In the previous article I’ve talked about how to generate the four Mothers of a Geomancy reading. These are the four geomantic figures you need in order to answer a question. As I discussed previously, the four Mothers, being actively created by you (or the questioner), represent your point of view, what you actively bring to the table. Afterward, we generate the four Daughters, which represent the consequence of your stance in the outside world around you.
This divides the Shield Chart into two halves: the right half, assigned to the querent or to what speaks in favor of the querent getting his wish; and the left half, assigned to the quesited or to the obstacles. These are like thesis and antithesis: as soon as the thesis is given, the antithesis is called into being automatically. The right half, the querent’s side, culminates into the Right Witness, while the left side culminates into the Left Witness. Here, the separation between thesis and antithesis reaches its apex, and can no longer be carried further, and must therefore be resolved. This is done by adding the Witnesses to form the Judge. This is the only figure in the chart that encompasses both right and left side, which is why the term “Judge” is fitting: the Judge must see the whole picture and take it into account in order to rule fairly.
Let us start with the Four Mothers, and let’s derive the Four Daughters from them.

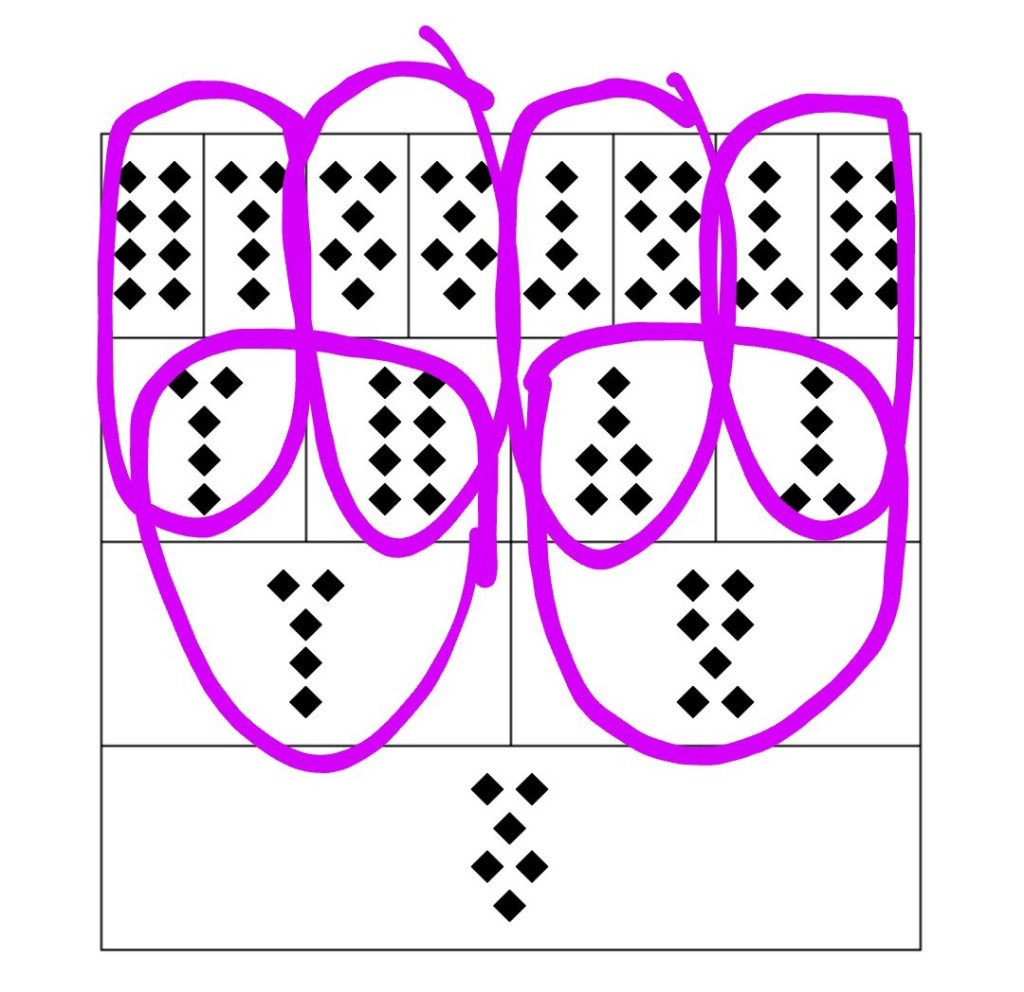
Above you find the Four Mothers. These are seen from right to left. To obtain the first daughter, we need to take into account the first row of points in each of the four Mothers. In the example above, the first row of the first Mother has two points, the first row of the second Mother has one point, the first row of the third Mother has two points and the first row of the fourth Mother has one point. This means that the first Daughter is going to be formed of two points in the top row, one in the second, two in the third and again one in the fourth. The other three Daughters are formed in the exact same way, only, we take into account the corresponding row in the four Mothers (i.e., for the second Daughter, the second row of each of the four Mothers, for the third Daughter, the third row of each of the four Mothers, for the fourth Daughter, the fourth row of each of the four Mothers.) At this point, we have the base line of the Geomantic Shield.

From this base line, which encompasses the two sides of the shield, we begin a new kind of operation, which will allow us to obtain the four Nieces. This operation is called Geomantic Addition. This is a very simple formula. Take the first two Mothers as an example. Now add the number of points in the top row of each. The sum is three (two in the first Mother, one in the second Mother.) Three is an odd number, and odd numbers are represented by a single point. Therefore, the result of this Geomantic Addition is going to be a figure whose first row is occupied by a single dot rather than two. Now we go through the same process row by row. Only at the end, with the fourth and final row, do we find that the operation gives a different result: here, both the first and the second Mother are made up of two points, so the result is four. Four is even, and even is represented by two points.
| First Mother | Second Mother | First Niece |
| O O | O | O |
| O O | O | O |
| O O | O | O |
| O O | O O | O O |
In general, the process of Geomantic Addition can only yield four scenarios.
| First Variable | Second Variable | Number of Points | Odd/Even | Result |
| O O | O O | 4 | Even | O O |
| O O | O | 3 | Odd | O |
| O | O O | 3 | Odd | O |
| O | O | 2 | Even | O O |
By pairing first and second Mother together, we get the first Niece; third and fourth Mother yield the second Niece; first and second Daughter give us the third Niece; and third and fourth daughter result in the fourth and final Niece.

At this point, we go over the process once more, pairing up the first and second Niece to obtain the Right Witness and the third and fourth to get the Left Witness.

The final addition yields the Judge, which is the only figure of the Geomantic Shield to result from the Left and Right side of the Shield communicating with each other.

This completes the operation. It is customary to derive a sixteenth figure by adding the figure of the querent, i.e., usually the first Mother, with the Judge, but this sixteenth figure is often not explicitly drawn on the shield, though it might sometimes, and there are examples of it in the old literature.
Note: all images are from the App ‘Simple Geomancy’